There’s a lot of excitement about twisted bilayer graphene, which I wrote a bit about earlier.  We have been going back to basics and studying the band structure of these systems, using some of the models which have been largely accepted, at least in broad terms, to describe them.  These models take the form of two continuum coupled Dirac equations with a spatially periodic hopping term connecting them.  The first thorough early study was by Bistritzer and MacDonald back in 2011.  They discovered that (1) for nearly all angles the original Dirac points of persist, (2) at certain “magic” angles the Dirac velocity vanishes, and (3) near these magic angles the low energy bands become exceptionally narrow over the entire Brillouin zone.

What we showed in our recent preprint is that actually the vanishing Dirac velocity is just one of several topological phase transitions associated with merging/splitting/annihilation of Dirac points as the angle is varied.  The above video shows how these points move around the moiré Brillouin zone as the angle is varied, in a range of angles close to the first magic angle (about 1 degree).  The parameter shown at the upper right of the video is inversely proportional to the angle.  Please see our preprint for more details.

If you went to the American Physical Society March meeting this year, you probably heard about exciting experiments discovering correlated insulators and superconductivity in twisted bilayer graphene.   This is exciting because it seems like the first real observation of strong correlation physics in graphene outside the strong field quantum Hall regime.  The moiré patterns generated by twisting these layers are fascinating and is an intriguing “twist” on correlated electron theory as well.  You can gauge the fascination of theorists by this by checking out how many papers appeared rapidly on the topic since on the arXiv.

Thanks to my colleague Cenke Xu, who works very quickly, he and I were the first ones in this wave of theories.  Our work was very simple, and perhaps naïve in some ways, but it does give an idea of the richness that might occur in these systems.  We found that even a relatively simple model leads to topological superconductivity, which would be quite exciting if true.  Our paper was recently published in PRL, and you can find a Physics Viewpoint that discusses it as well.  I made the image in this post due to a request from the editors for this Viewpoint, but apparently they didn’t like it.  So instead I’m sharing it here.

My group is continuing to work on the subject, and I plan to post something on our more recent work soon.

Counter current heat exchange in a gull’s leg.  Art by Michael McNelly (after Ricklefs. 1990. Ecology. W.H. Freeman, New York).  Taken from this page

In biology class in high school, I learned that birds have a clever mechanism to help keep warm in winter.  They need to supply blood all the way down their bare legs to their feet.  This is potentially a way to lose a lot of heat, as it would be lost readily to the environment without any insulation.  However, in a bird’s leg, the artery in which blood flows down is positioned in contact with the vein that carries the blood back up, and heat is exchanged across the contact.  In that way most of the heat does not flow down the leg, and the lower portion of the leg maintains a much lower temperature where it does not lose heat.  This is called counter current heat exchange.

My group recently stumbled across an analog of this phenomena in a very different venue – a type of Hall effect in a quantum spin liquid.  This was prompted by a beautiful experiment by Kasahara et al, just published in Nature , reporting the discovery of a quantized thermal Hall effect in the material -RuCl₃.  A thermal Hall effect means that some heat moves perpendicular to an applied temperature gradient, or conversely, that a temperature gradient appears perpendicular to the flow of heat.  You can imagine there is some relation to the bird’s leg, in which the main heat flow is vertically up and down the leg, but heat also passes horizontally from the artery to the vein.  In the experiment, a heat current is applied along the x direction of a sample, and a temperature gradient develops along the y axis.  The remarkable thing – not present in the bird – is that the magnitude of the temperature difference divided by the heat current is quantized.

Quantization of the thermal Hall effect was predicted a long time ago for systems that possess chiral edge states, like those in the quantum Hall effect (which is a similar but much easier to measure effect involving electrical current and voltage rather than heat current and temperature).  However, the theory behind the thermal Hall effect presumed that these edge states are the only things carrying heat.  In the experiment by Kasahara et al, however, it is clear that most of the heat is actually being carried by motions of the atoms that make up the crystal, rather than chiral edge states.  So the theory needed to be reconsidered.   A few of us – Mengxing Ye, Gábor Halász, Lucile Savary, and I – developed a theory of the thermal Hall effect including the lattice.  What we found was that the approximate quantization of the thermal Hall effect could be explained if the lattice acts as a counter current heat exchanger between two edge states that play the role of the artery and the vein in the bird.  It was rather surprising to us, and indeed we found that actually the lattice’s involvement in heat transfer helps to observe the effect.

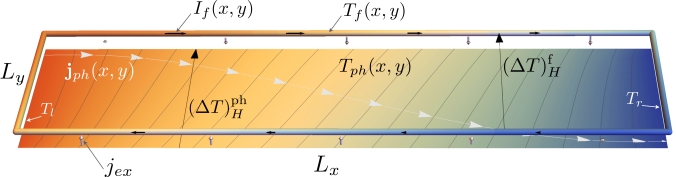
Schematic of the counter current heat exchange in the thermal Hall effect.  An edge state at the upper and lower edge (and the boundaries) is shown as a tube, with horizontal arrows showing the flow of heat in the edges.  Vertical arrows show the heat flow from the edge into the bulk lattice, which acts as the medium to exchange heat between the edges.  For an explanation of all the other labels, see our paper.

This is a rather quick summary.  I actually wrote a commentary on the experiment in the journal club for condensed matter physics, which you can read here.  This explains the quantum context more, and why it is such a cool discovery.  You can also read our paper on the arXiv.   The final version has appeared in Physical Review Letters.